G2

Introduction to Regression Curve Chart

A regression curve chart is a statistical chart that adds regression curves on top of scatter plots to show mathematical relationships between two or more variables and predict trends. Regression curves use mathematical algorithms to fit data points, finding the best functional relationship between variables, helping analyze the inherent patterns in data and make trend predictions.

Regression curve charts combine the data distribution display capability of scatter plots with the predictive functionality of mathematical modeling. They not only intuitively show the distribution of data points but also reveal potential relationships between variables through fitted curves, making them an important tool in data analysis and scientific research.

Common regression types include linear regression, polynomial regression, exponential regression, logarithmic regression, etc. Different regression methods are suitable for different data patterns and relationship types.

English Name: Regression Curve Chart

Components of Regression Curve Chart

Chart Type	Regression Curve Chart
Suitable Data	Two continuous data fields: one independent variable field, one dependent variable field
Function	Display mathematical relationships between variables, identify data trends, perform predictive analysis
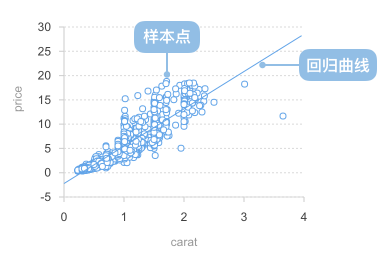
Data-Graphics Mapping	Independent variable field maps to horizontal axis position Dependent variable field maps to vertical axis position Data points show original observations Regression curve shows fitted mathematical relationship
Suitable Data Amount	10-1000 data points, enough data points are needed for effective regression analysis

Components:

Scatter Points: Points representing original data observations
Regression Curve: Trend line fitted through mathematical algorithms
X-axis: Horizontal coordinate axis, usually representing the independent variable
Y-axis: Vertical coordinate axis, usually representing the dependent variable
Regression Equation: Mathematical formula describing variable relationships
Coefficient of Determination (R²): Indicator measuring the goodness of fit of the regression model

Application Scenarios for Regression Curve Chart

Suitable Scenarios

Example 1: Linear Relationship Data Analysis

Linear regression is suitable for showing linear relationships between two variables, such as height vs. weight, temperature vs. sales, etc.

import { Chart } from '@antv/g2';
import { regressionLinear } from 'd3-regression';

const chart = new Chart({
  container: 'container',
  theme: 'classic',
});

chart.options({
  type: 'view',
  autoFit: true,
  data: {
    type: 'fetch',
    value: 'https://assets.antv.antgroup.com/g2/linear-regression.json',
  },
  children: [
    {
      type: 'point',
      encode: { x: (d) => d[0], y: (d) => d[1] },
      scale: { x: { domain: [0, 1] }, y: { domain: [0, 5] } },
      style: { fillOpacity: 0.75, fill: '#1890ff' },
    },
    {
      type: 'line',
      data: {
        transform: [
          {
            type: 'custom',
            callback: regressionLinear(),
          },
        ],
      },
      encode: { x: (d) => d[0], y: (d) => d[1] },
      style: { stroke: '#30BF78', lineWidth: 2 },
      labels: [
        {
          text: 'y = 1.7x + 3.01',
          selector: 'last',
          position: 'right',
          textAlign: 'end',
          dy: -8,
        },
      ],
      tooltip: false,
    },
  ],
  axis: {
    x: { title: 'Independent Variable X' },
    y: { title: 'Dependent Variable Y' },
  },
});

chart.render();

Description:

Scatter points show original data distribution
Linear regression line reveals linear relationship between two variables
Regression equation provides precise mathematical description
Suitable for prediction and trend analysis

Example 2: Non-linear Relationship - Quadratic Regression

When data shows a curved trend, quadratic regression (parabola) can be used to fit the data.

import { Chart } from '@antv/g2';
import { regressionQuad } from 'd3-regression';

const chart = new Chart({
  container: 'container',
  theme: 'classic',
});

const data = [
  { x: -4, y: 5.2 },
  { x: -3, y: 2.8 },
  { x: -2, y: 1.5 },
  { x: -1, y: 0.8 },
  { x: 0, y: 0.5 },
  { x: 1, y: 0.8 },
  { x: 2, y: 1.5 },
  { x: 3, y: 2.8 },
  { x: 4, y: 5.2 },
];

chart.options({
  type: 'view',
  autoFit: true,
  data,
  children: [
    {
      type: 'point',
      encode: { x: 'x', y: 'y' },
      style: { fillOpacity: 0.75, fill: '#1890ff' },
    },
    {
      type: 'line',
      data: {
        transform: [
          {
            type: 'custom',
            callback: regressionQuad()
              .x((d) => d.x)
              .y((d) => d.y)
              .domain([-4, 4]),
          },
        ],
      },
      encode: { x: (d) => d[0], y: (d) => d[1] },
      style: { stroke: '#30BF78', lineWidth: 2 },
      labels: [
        {
          text: 'y = 0.3x² + 0.5',
          selector: 'last',
          textAlign: 'end',
          dy: -8,
        },
      ],
      tooltip: false,
    },
  ],
  axis: {
    x: { title: 'Independent Variable X' },
    y: { title: 'Dependent Variable Y' },
  },
});

chart.render();

Description:

Quadratic regression is suitable for displaying data relationships with parabolic characteristics
Can capture curved trends and extreme points in data
Commonly used for non-linear relationship analysis in physics and economics

Example 3: Exponential Growth Trend Analysis

Exponential regression is suitable for displaying exponential growth or decay data patterns, such as population growth, bacterial reproduction, etc.

import { Chart } from '@antv/g2';
import { regressionExp } from 'd3-regression';

const chart = new Chart({
  container: 'container',
  theme: 'classic',
});

chart.options({
  type: 'view',
  autoFit: true,
  data: {
    type: 'fetch',
    value: 'https://assets.antv.antgroup.com/g2/exponential-regression.json',
  },
  children: [
    {
      type: 'point',
      encode: { x: (d) => d[0], y: (d) => d[1] },
      scale: {
        x: { domain: [0, 18] },
        y: { domain: [0, 100000] },
      },
      style: { fillOpacity: 0.75, fill: '#1890ff' },
    },
    {
      type: 'line',
      data: {
        transform: [
          {
            type: 'custom',
            callback: regressionExp(),
          },
        ],
      },
      encode: {
        x: (d) => d[0],
        y: (d) => d[1],
        shape: 'smooth',
      },
      style: { stroke: '#30BF78', lineWidth: 2 },
      labels: [
        {
          text: 'y = 3477.32e^(0.18x)\nR² = 0.998',
          selector: 'last',
          textAlign: 'end',
          dy: -20,
        },
      ],
      tooltip: false,
    },
  ],
  axis: {
    x: { title: 'Time' },
    y: {
      title: 'Value',
      labelFormatter: '~s',
    },
  },
});

chart.render();

Description:

Exponential regression is suitable for analyzing rapid growth or decay trends
R² value close to 1 indicates very good fit
Commonly used for predicting future trends with exponential characteristics

Unsuitable Scenarios

Example 1: Insufficient Data Points

When there are too few data points, regression analysis may not be reliable and can lead to misleading conclusions.

import { Chart } from '@antv/g2';
import { regressionLinear } from 'd3-regression';

const chart = new Chart({
  container: 'container',
  theme: 'classic',
});

const insufficientData = [
  { x: 1, y: 2 },
  { x: 3, y: 4 },
  { x: 5, y: 3 },
];

chart.options({
  type: 'view',
  autoFit: true,
  data: insufficientData,
  children: [
    {
      type: 'point',
      encode: { x: 'x', y: 'y' },
      style: {
        fillOpacity: 0.8,
        fill: '#ff4d4f',
        r: 8,
      },
    },
    {
      type: 'line',
      data: {
        transform: [
          {
            type: 'custom',
            callback: regressionLinear()
              .x((d) => d.x)
              .y((d) => d.y),
          },
        ],
      },
      encode: { x: (d) => d[0], y: (d) => d[1] },
      style: {
        stroke: '#ff4d4f',
        lineWidth: 2,
        strokeDasharray: [4, 4],
      },
      tooltip: false,
    },
  ],
  axis: {
    x: { title: 'Variable X' },
    y: { title: 'Variable Y' },
  },
  title: 'Unsuitable: Regression Analysis with Too Few Data Points',
});

chart.render();

Problem Description:

Only 3 data points, insufficient sample size
Limited reliability and predictive capability of the regression line
Easily affected by outliers
Recommend at least 10 or more data points for regression analysis

Example 2: Data with No Clear Correlation

When there is no clear correlation between two variables, forcing a regression line may mislead the analysis.

import { Chart } from '@antv/g2';
import { regressionLinear } from 'd3-regression';

const chart = new Chart({
  container: 'container',
  theme: 'classic',
});

// Generate randomly distributed data (no correlation)
const randomData = Array.from({ length: 30 }, (_, i) => ({
  x: Math.random() * 10,
  y: Math.random() * 10,
}));

chart.options({
  type: 'view',
  autoFit: true,
  data: randomData,
  children: [
    {
      type: 'point',
      encode: { x: 'x', y: 'y' },
      style: {
        fillOpacity: 0.8,
        fill: '#ff4d4f',
        r: 6,
      },
    },
    {
      type: 'line',
      data: {
        transform: [
          {
            type: 'custom',
            callback: regressionLinear()
              .x((d) => d.x)
              .y((d) => d.y),
          },
        ],
      },
      encode: { x: (d) => d[0], y: (d) => d[1] },
      style: {
        stroke: '#ff4d4f',
        lineWidth: 2,
        strokeDasharray: [4, 4],
      },
      labels: [
        {
          text: 'R² ≈ 0.02 (extremely low)',
          selector: 'last',
          textAlign: 'end',
          dy: -8,
        },
      ],
      tooltip: false,
    },
  ],
  axis: {
    x: { title: 'Variable X' },
    y: { title: 'Variable Y' },
  },
  title: 'Unsuitable: Data with No Correlation',
});

chart.render();

Problem Description:

Data points show random distribution with no clear trend pattern
Extremely low R² value indicates the regression model can hardly explain variable relationships
Regression line has no practical meaning and may mislead decision-making
Should perform correlation analysis first to confirm relationships between variables before regression

Extensions of Regression Curve Chart

Polynomial Regression

When data shows complex curved trends, polynomial regression can be used to fit more complex curves.

import { Chart } from '@antv/g2';
import { regressionPoly } from 'd3-regression';

const chart = new Chart({
  container: 'container',
  theme: 'classic',
});

const polynomialData = [
  { x: 0, y: 140 },
  { x: 1, y: 149 },
  { x: 2, y: 159.6 },
  { x: 3, y: 159 },
  { x: 4, y: 155.9 },
  { x: 5, y: 169 },
  { x: 6, y: 162.9 },
  { x: 7, y: 169 },
  { x: 8, y: 180 },
];

chart.options({
  type: 'view',
  autoFit: true,
  data: polynomialData,
  children: [
    {
      type: 'point',
      encode: { x: 'x', y: 'y' },
      style: { fillOpacity: 0.75, fill: '#1890ff' },
    },
    {
      type: 'line',
      data: {
        transform: [
          {
            type: 'custom',
            callback: regressionPoly()
              .x((d) => d.x)
              .y((d) => d.y),
          },
        ],
      },
      encode: {
        x: (d) => d[0],
        y: (d) => d[1],
        shape: 'smooth',
      },
      style: { stroke: '#30BF78', lineWidth: 2 },
      labels: [
        {
          text: 'y = 0.24x³ - 3.00x² + 13.45x + 139.77\nR² = 0.92',
          selector: 'last',
          textAlign: 'end',
          dx: -8,
          dy: -20,
        },
      ],
      tooltip: false,
    },
  ],
  axis: {
    x: { title: 'Time' },
    y: { title: 'Value' },
  },
});

chart.render();

Description:

Polynomial regression can fit complex curved relationships
Suitable for handling data with multiple peaks and valleys
Need to be careful to avoid overfitting problems

Logarithmic Regression

Logarithmic regression is suitable for data patterns where the growth rate gradually slows down.

import { Chart } from '@antv/g2';
import { regressionLog } from 'd3-regression';

const chart = new Chart({
  container: 'container',
  theme: 'classic',
});

chart.options({
  type: 'view',
  autoFit: true,
  data: {
    type: 'fetch',
    value: 'https://assets.antv.antgroup.com/g2/logarithmic-regression.json',
  },
  children: [
    {
      type: 'point',
      encode: { x: 'x', y: 'y' },
      scale: { x: { domain: [0, 35] } },
      style: { fillOpacity: 0.75, fill: '#1890ff' },
    },
    {
      type: 'line',
      data: {
        transform: [
          {
            type: 'custom',
            callback: regressionLog()
              .x((d) => d.x)
              .y((d) => d.y)
              .domain([0.81, 35]),
          },
        ],
      },
      encode: {
        x: (d) => d[0],
        y: (d) => d[1],
        shape: 'smooth',
      },
      style: { stroke: '#30BF78', lineWidth: 2 },
      labels: [
        {
          text: 'y = 0.881·ln(x) + 4.173\nR² = 0.958',
          selector: 'last',
          textAlign: 'end',
          dy: -20,
        },
      ],
      tooltip: false,
    },
  ],
  axis: {
    x: { title: 'Variable X' },
    y: { title: 'Variable Y' },
  },
});

chart.render();

Description:

Logarithmic regression is suitable for showing diminishing marginal effects
Commonly used for analyzing learning curves, diminishing returns scenarios
Can handle data patterns with gradually decreasing growth rates

Multi-Variable Regression Comparison

Multiple regression methods can be compared in the same chart to show their comparative effects.

import { Chart } from '@antv/g2';
import {
  regressionLinear,
  regressionQuad,
  regressionPoly,
} from 'd3-regression';

const chart = new Chart({
  container: 'container',
  theme: 'classic',
});

const comparisonData = [
  { x: 1, y: 2.1 },
  { x: 2, y: 3.9 },
  { x: 3, y: 6.8 },
  { x: 4, y: 10.2 },
  { x: 5, y: 15.1 },
  { x: 6, y: 21.5 },
  { x: 7, y: 29.8 },
  { x: 8, y: 40.2 },
];

chart.options({
  type: 'view',
  autoFit: true,
  data: comparisonData,
  children: [
    {
      type: 'point',
      encode: { x: 'x', y: 'y' },
      style: {
        fillOpacity: 0.8,
        fill: '#1890ff',
        r: 6,
      },
    },
    // Linear regression
    {
      type: 'line',
      data: {
        transform: [
          {
            type: 'custom',
            callback: regressionLinear()
              .x((d) => d.x)
              .y((d) => d.y),
          },
        ],
      },
      encode: { x: (d) => d[0], y: (d) => d[1] },
      style: {
        stroke: '#ff4d4f',
        lineWidth: 2,
        strokeDasharray: [4, 4],
      },
      tooltip: false,
    },
    // Quadratic regression
    {
      type: 'line',
      data: {
        transform: [
          {
            type: 'custom',
            callback: regressionQuad()
              .x((d) => d.x)
              .y((d) => d.y),
          },
        ],
      },
      encode: { x: (d) => d[0], y: (d) => d[1] },
      style: {
        stroke: '#30BF78',
        lineWidth: 2,
      },
      tooltip: false,
    },
  ],
  axis: {
    x: { title: 'Variable X' },
    y: { title: 'Variable Y' },
  },
  legends: [
    {
      color: {
        position: 'top',
        itemMarker: (color, index) => {
          if (index === 0)
            return {
              symbol: 'line',
              style: { stroke: '#ff4d4f', strokeDasharray: [4, 4] },
            };
          if (index === 1)
            return { symbol: 'line', style: { stroke: '#30BF78' } };
        },
        data: [
          { color: '#ff4d4f', value: 'Linear Regression' },
          { color: '#30BF78', value: 'Quadratic Regression' },
        ],
      },
    },
  ],
});

chart.render();

Description:

Can simultaneously display the fitting effects of multiple regression methods
Helps choose the regression model that best fits the data characteristics
Find the best fitting method through comparative analysis

Comparison with Other Charts

Regression Curve Chart vs Scatter Plot

Regression curve charts add mathematical modeling and prediction functionality on top of scatter plots
Scatter plots focus on displaying data distribution and correlation, while regression curve charts emphasize trend analysis and prediction
Choose regression curve charts when trend prediction is needed, choose scatter plots when only data distribution observation is required

Regression Curve Chart vs Line Chart

Regression curve charts are based on mathematical model fitting, while line charts directly connect data points
Regression curve charts can smooth noise and make predictions, while line charts accurately reflect each data point
Choose regression curve charts when trend pattern analysis is needed, choose line charts when precise change display is required

G2

Regression Curve Chart

Introduction to Regression Curve Chart

Components of Regression Curve Chart

Application Scenarios for Regression Curve Chart

Suitable Scenarios

Unsuitable Scenarios

Extensions of Regression Curve Chart

Polynomial Regression

Logarithmic Regression

Multi-Variable Regression Comparison

Comparison with Other Charts

Regression Curve Chart vs Scatter Plot

Regression Curve Chart vs Line Chart

Similar Charts

Category