G2

Introduction to Distribution Curve

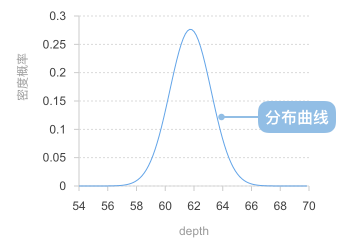
A distribution curve is a statistical chart used to display the frequency distribution of data, intuitively reflecting the distribution density and central tendency of data across different value intervals through smooth curve forms. It is an important visualization tool for understanding data distribution characteristics and identifying data patterns.

Distribution curves are particularly suitable for exploratory data analysis, comparing distributions across multiple groups, data quality checking, and identifying statistical distribution characteristics, making them important tools in statistical analysis and data science.

English Name: Distribution Curve, Frequency Curve, Density Curve

Components of Distribution Curve

A distribution curve consists of the following elements:

Horizontal axis: represents the independent variable
Vertical axis: represents the dependent variable
Distribution curve representing probability distribution

Application Scenarios for Distribution Curves

Suitable Scenarios

Example 1: Displaying distribution characteristics of normal distribution data

Distribution curves are very suitable for displaying normal distribution data, clearly showing the central tendency, symmetry, and distribution shape of the data.

import { Chart } from '@antv/g2';

// Generate normal distribution data
const generateNormalData = (count, mean, std) => {
  const data = [];
  for (let i = 0; i < count; i++) {
    // Use Box-Muller transform to generate normal distribution data
    const u1 = Math.random();
    const u2 = Math.random();
    const z0 = Math.sqrt(-2 * Math.log(u1)) * Math.cos(2 * Math.PI * u2);
    data.push({ value: mean + std * z0 });
  }
  return data;
};

const chart = new Chart({
  container: 'container',
  theme: 'classic',
});

chart.options({
  type: 'line',
  data: {
    value: generateNormalData(1000, 100, 15),
    transform: [
      {
        type: 'custom',
        callback: (data) => {
          // Extract numerical data
          const values = data.map(d => d.value).filter(v => !isNaN(v));
          
          // Calculate data range
          const min = Math.min(...values);
          const max = Math.max(...values);
          const binCount = 30;
          const binWidth = (max - min) / binCount;
          
          // Create bins
          const bins = Array.from({ length: binCount }, (_, i) => ({
            x0: min + i * binWidth,
            x1: min + (i + 1) * binWidth,
            count: 0,
          }));
          
          // Count frequency for each bin
          values.forEach(value => {
            const binIndex = Math.min(
              Math.floor((value - min) / binWidth),
              binCount - 1
            );
            bins[binIndex].count++;
          });
          
          // Calculate frequency density and generate curve data
          const total = values.length;
          return bins.map(bin => ({
            x: (bin.x0 + bin.x1) / 2, // Bin center point
            y: bin.count / total, // Frequency density
            frequency: bin.count,
            range: `${bin.x0.toFixed(1)}-${bin.x1.toFixed(1)}`,
          }));
        },
      },
    ],
  },
  encode: {
    x: 'x',
    y: 'y',
    shape: 'smooth',
  },
  style: {
    lineWidth: 3,
    stroke: '#1890ff',
  },
  axis: {
    x: { title: 'Measured Value' },
    y: { title: 'Frequency Density' },
  },
  tooltip: {
    title: (d) => `Range: ${d.range}`,
    items: [
      { field: 'frequency', name: 'Frequency' },
      { field: 'y', name: 'Frequency Density', valueFormatter: '.3f' },
    ],
  },
});

chart.render();

Description:

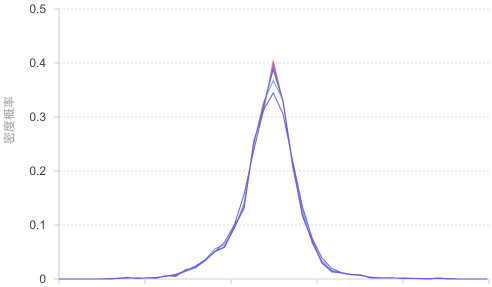
Displays the classic bell-shaped normal distribution curve
Clearly observes the symmetry and central tendency of the data
Suitable for data analysis in quality control, biostatistics, psychological measurement, and other fields

Example 2: Comparative analysis of multiple group distributions

When comparing data distributions under different conditions or groups, distribution curves can intuitively show distribution differences between groups.

import { Chart } from '@antv/g2';

const chart = new Chart({
  container: 'container',
  theme: 'classic',
});

chart.options({
  type: 'line',
  data: {
    type: 'fetch',
    value: 'https://assets.antv.antgroup.com/g2/species.json',
    transform: [
      {
        type: 'custom',
        callback: (data) => {
          // Group data by species
          const groups = {};
          data.forEach(d => {
            if (!groups[d.species]) groups[d.species] = [];
            groups[d.species].push(d.y);
          });
          
          const binCount = 20;
          const results = [];
          
          // Create distribution curve data for each species
          Object.entries(groups).forEach(([species, values]) => {
            const filteredValues = values.filter(v => !isNaN(v));
            if (filteredValues.length === 0) return;
            
            const min = Math.min(...filteredValues);
            const max = Math.max(...filteredValues);
            const binWidth = (max - min) / binCount;
            
            // Create bins
            const bins = Array.from({ length: binCount }, (_, i) => ({
              x0: min + i * binWidth,
              x1: min + (i + 1) * binWidth,
              count: 0,
            }));
            
            // Count frequencies
            filteredValues.forEach(value => {
              const binIndex = Math.min(
                Math.floor((value - min) / binWidth),
                binCount - 1
              );
              bins[binIndex].count++;
            });
            
            // Generate curve data
            const total = filteredValues.length;
            bins.forEach(bin => {
              results.push({
                x: (bin.x0 + bin.x1) / 2,
                y: bin.count / total,
                species,
                frequency: bin.count,
                range: `${bin.x0.toFixed(2)}-${bin.x1.toFixed(2)}`,
              });
            });
          });
          
          return results;
        },
      },
    ],
  },
  encode: {
    x: 'x',
    y: 'y',
    color: 'species',
    shape: 'smooth',
  },
  style: {
    lineWidth: 2,
    strokeOpacity: 0.8,
  },
  axis: {
    x: { title: 'Petal Length' },
    y: { title: 'Frequency Density' },
  },
  legend: {
    color: {
      title: 'Species',
      position: 'right',
    },
  },
  tooltip: {
    title: (d) => `${d.species} - Range: ${d.range}`,
    items: [
      { field: 'frequency', name: 'Frequency' },
      { field: 'y', name: 'Frequency Density', valueFormatter: '.3f' },
    ],
  },
});

chart.render();

Description:

Compares distribution characteristics of multiple groups through curves of different colors
Facilitates identification of distribution centers, shapes, and dispersion of each group
Suitable for A/B testing analysis, experimental control group comparisons, market segmentation analysis, and other scenarios

Unsuitable Scenarios

Example 1: Poor effectiveness with insufficient data

When there are too few data points, binning statistics may not be accurate enough, and the generated distribution curve may not accurately reflect true distribution characteristics.

import { Chart } from '@antv/g2';

// Simulate small amount of data
const smallData = [
  12, 15, 13, 14, 16, 18, 11, 17, 15, 13
];

const chart = new Chart({
  container: 'container',
  theme: 'classic',
  height: 250,
});

chart.options({
  type: 'point',
  data: smallData.map((value, index) => ({ index: index + 1, value })),
  encode: {
    x: 'index',
    y: 'value',
    size: 6,
  },
  style: {
    fill: '#1890ff',
    fillOpacity: 0.8,
  },
  axis: {
    x: { title: 'Data Point Index' },
    y: { title: 'Value' },
  },
  title: 'Scatter plot recommended for small datasets',
});

chart.render();

Problem Description:

When there are too few data points (less than 30), each interval has too little data after binning
The generated distribution curve may show artificial fluctuations and irregular shapes
Cannot accurately reflect true data distribution characteristics
Recommend using scatter plots, box plots, or increasing data collection

Example 2: Discrete categorical data is not applicable

For discrete categorical data, continuous distribution curves have no practical meaning because there is no continuity relationship between categories.

import { Chart } from '@antv/g2';

// Discrete categorical data
const discreteData = [
  { category: 'Product A', sales: 45 },
  { category: 'Product B', sales: 67 },
  { category: 'Product C', sales: 33 },
  { category: 'Product D', sales: 52 },
  { category: 'Product E', sales: 28 },
];

const chart = new Chart({
  container: 'container',
  theme: 'classic',
  height: 250,
});

chart.options({
  type: 'interval',
  data: discreteData,
  encode: {
    x: 'category',
    y: 'sales',
    color: 'category',
  },
  style: {
    fillOpacity: 0.8,
  },
  axis: {
    x: { title: 'Product Category' },
    y: { title: 'Sales Quantity' },
  },
  title: 'Bar chart recommended for categorical data',
});

chart.render();

Problem Description:

No continuity relationship exists between categorical data; forcing connections would be misleading
Distribution curves cannot express the true meaning of categorical data
Bar charts can more accurately express comparison relationships in categorical data
Suitable for using discrete chart types such as bar charts and pie charts

Comparison with Other Charts

Distribution Curve vs Histogram

Distribution curves display continuous frequency distribution through smooth curves, emphasizing overall trends
Histograms display frequency distribution through rectangular bars with clear interval boundaries
Distribution curves are more suitable for displaying overall distribution shape and trend identification
Histograms are more suitable for precise frequency statistics and interval analysis

Distribution Curve vs Violin Plot

Distribution curves focus on displaying the curve shape of frequency distribution
Violin plots combine density distribution with statistical summary information from box plots
Distribution curves are more suitable for pure distribution shape analysis and multi-group comparisons
Violin plots are more suitable for scenarios requiring statistical summary information

Distribution Curve vs Line Chart

Distribution curves are based on frequency statistics, displaying data distribution characteristics
Line charts show data change trends over time or sequence
Distribution curves are suitable for statistical analysis and distribution exploration
Line charts are suitable for time series analysis and trend tracking

Distribution Curve